Loan Amortization Calculator
Tools to help you make informed decisions
The amortization calculator or loan amortization calculator is a handy tool that not only helps you to compute the payment of any amortized loan, but also gives you a detailed picture of the loan in question through its amortization schedule.
You can also study the loan amortization schedule on a monthly and yearly basis and follow the progression of the balances of the loan in a dynamic amortization chart. If you read on, you can learn what the amortization definition is, as well as the amortization formula, with relevant details on this topic.
Get expert guidance from a Capital Markets Advisor
We look forward to serving you
call us
800-616-2050
Email Us
What is amortization?
The repayment of most loans is realized by a series of even payments made on a regular basis. The popular term in finance to describe loans with such a repayment schedule is an amortized loan. Accordingly, we may phrase the amortization definition as “a loan paid off by equal periodic installments over a specified term”. Typically, the details of the repayment schedule are summarized in the amortization schedule, which shows how the payment is divided between the interest (computed on the outstanding balance) and the principal. The amortization chart might also represent the unpaid balance at the end of each period. A few examples of loan amortization are automobile loans, home mortgage loans, student loans, and many business loans.
As in general the core concept that governs financial instruments is the time value of money, the loan amortization is similarly strongly connected to the present value and future value of money. More specifically, there is a concept called the present value of annuity that conforms the most to the loan amortization framework.
To see why, let’s consider the following simple example. Suppose you borrow $1,000, which you need to repay in five equal parts due at the end of every year (the amortization term is five years with a yearly payment frequency). The lender charges you 12 percent interest, that is calculated on the outstanding balance at the beginning of each year (therefore, the compounding frequency is yearly).
The illustration below represents the timeline of this example, where PMT is the yearly payment or installment. To find PMT, we need to find a value such that the sum of their present values equals the loan amount: $1,000.

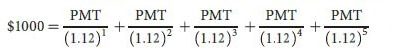
The solution of this equation involves complex mathematics (you may check out the IRR calculator for more on its background); so, it’s easier to rely on our amortization calculator. After setting the parameters according to the above example, we get the result for the periodic payment, which is $277.41.
Loan amortization schedule – the amortization table
The specific feature of amortized loans is that each payment is the combination of two parts: the repayment of principal and the interest on the remaining principal. The amortization chart below, which appears in the calculator as well, represents the payment schedule of the previous example. As you can see, the interest payments are typically high in early periods and decrease over time, while the reverse is true for the principal payments. The lowering interest amount is matched by the increasing amount of principal so that the total loan payment remains the same over the loan term.
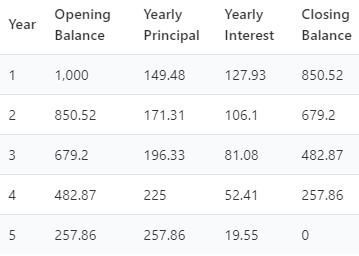
The large unpaid principal balance at the beginning of the loan term means that most of the total payment is interest, with a smaller portion of the principal being paid. Since the principal amount being paid off is comparably low at the beginning of the loan term, the unpaid balance of the loan decreases slowly. As the loan payoff proceeds, the unpaid balance declines, which gradually reduces the interest obligations, making more room for a higher principal repayment. Logically, the higher the weight of the principal part in the periodic payment, the higher the rate of decline in the unpaid balance.
It may be easier to understand this concept if it is displayed as a graph of the relevant balances, which is why this option is also displayed in the calculator.
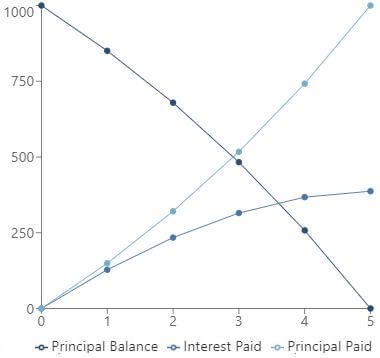
An amortized loan is a form of credit where the loan is paid off with equal, consecutive payments over a specified period. An amortization schedule shows the structure of these consecutive payments: the interest paid, the principal repaid, and the unpaid balance at the end of each period, which must reach zero during the amortization term.
What is the amortization formula?
As you have now gained some insight into the logic behind the amortized loan structure, in this section you can learn two basic formulas employed in our amortization calculator:
- Monthly repayment formula
P = (A * i * (1 + i)t)) / ((1 + i)t - 1)
- Unpaid balance formula
B = A * ((1 + i)t) - P / i * ((1 + i)t - 1)
Where
P– monthly payment amountA– loan repayment amounti– periodic interest ratet– number of periodsB– unpaid balance
Amortization calculator with extra payments
It is worth knowing that the amortization term doesn’t necessarily equal to the original loan term; that is, you may pay off the principal faster than the time estimated with the periodic payments based on the initial amortization term. An obvious way to shorten the amortization term is to decrease the unpaid principal balance faster than set out in the original repayment plan. You may do so by a lump sum advance payment, or by increasing the periodic installments.
In this calculator, you can set an extra payment, which raises the regular payment amount. The power of such an extra payment is that its amount is directly allocated to the repayment of the loan amount. In this way, the principal balance decreases in an accelerating fashion, resulting in a shorter amortization term and a considerably lower total interest burden.
The beneficial effect of extra payments is especially profound when the initial loan term is relatively long, such as most mortgage loans. When you set the extra payment in this calculator, you can follow and compare the progress of new balances with the original plan on the dynamic chart, and the amortization schedule with extra payment.
How to calculate DSCR?
Our debt service coverage ratio calculator uses the following formula:
where:
- DSCR – Debt service coverage ratio;
- NOI – Monthly net operating income; and
- debt service – Monthly payment towards paying off your debts.
You can input the value of NOI directly in this DSCR calculator or head to our net effective rent calculator for a more detailed calculation scheme.
Alternatively, you can open the advanced mode to determine NOI according to the equation:
In this formula:
- GI – Gross income – the monthly rent paid by your tenants;
- expenses – Monthly expenses for maintenance, repairs, or cleaning, expressed as a percentage of the gross income; and
- vacancy – Vacancy rate (how often you don’t have a tenant for the apartment), expressed as a percentage of the gross income.
Our debt service coverage ratio lets you easily determine your debt service.
Contact Us
The team at INSIGNIA Financial Services is available to discuss your real estate or small business lending needs and we’re available to answer any questions you may have about our financing solutions.
call us
800-616-2050
Send us a secure message using the form below.
Operations Center
1020 Milwaukee Ave, # 230
Deerfield, Illinois 60015
